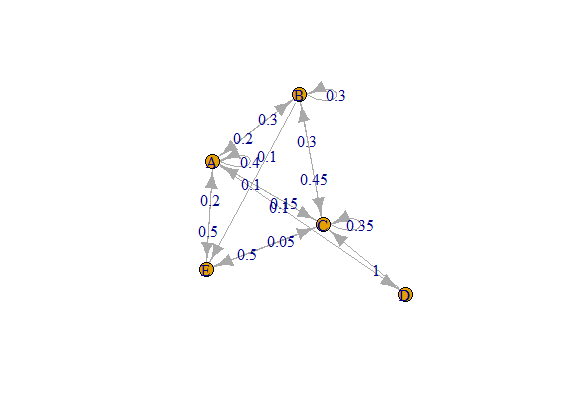
Les processus stochastiques sont des modèles mathématiques utilisés pour décrire et étudier l'évolution aléatoire de systèmes au fil du temps. Ils sont largement utilisés dans de nombreux domaines, notamment les finances, l'économie, la physique, la biologie, l'ingénierie, et bien d'autres.
En termes simples, un processus stochastique est une collection de variables aléatoires indexées par le temps (ou par un autre paramètre). Chaque variable aléatoire représente l'état du système à un moment donné, et ces états évoluent selon des règles probabilistes qui dépendent souvent des états précédents.
Les chaînes de Markov sont utilisées dans divers domaines tels que l'économie, la modélisation des files d'attente, la biologie pour modéliser les processus évolutifs, la reconnaissance de motifs dans les signaux, etc.
Voici quelques exemples d'applications des processus stochastiques :
- Finance et Économie : Les modèles de prix d'actifs financiers comme le mouvement Brownien géométrique (GBM) sont des processus stochastiques largement utilisés pour modéliser les fluctuations des prix des actifs.
- Télécommunications : Les processus stochastiques sont utilisés pour modéliser le trafic dans les réseaux de communication, aidant à concevoir des systèmes de transmission de données plus efficaces.
- Biologie : En biologie, ces processus sont utilisés pour modéliser l'évolution des populations, la diffusion des molécules dans les cellules, ou encore les mutations génétiques aléatoires.
- Ingénierie : En ingénierie, les processus stochastiques peuvent être utilisés pour modéliser la dégradation des matériaux, la fiabilité des systèmes, ou encore pour prédire les pannes.
- Météorologie et Climatologie : Les modèles climatiques utilisent des processus stochastiques pour simuler les variations météorologiques sur de longues périodes.
- Traitement du Signal : En traitement du signal, les processus stochastiques sont utilisés pour modéliser le bruit, les signaux aléatoires et les processus de filtrage.
- L'application typique d'une chaîne de Markov est par exemple la modélisation du temps passé dans différents états, comme les transitions entre les états météorologiques (ensoleillé, nuageux, pluvieux) ou les états du marché financier (hausse, baisse, stagnation) où la probabilité de passer d'un état à un autre dépend uniquement de l'état actuel et non de l'historique complet des états précédents.
En général, les processus stochastiques fournissent un cadre mathématique puissant pour modéliser et comprendre les phénomènes aléatoires qui évoluent dans le temps, ce qui permet de prendre des décisions plus éclairées dans de nombreux domaines.
- Enseignant: BENDJEDDOU SARA
